? ?? ?孩子、家长都需要的心理测试：情商测试、专业心理健康测评、专注力评估、学生考试心理健康测试、家长胜任能力测试等12项。

? ? ?点击下图即可进入测试，测试结果可以发到您的微信，为您的决策提供帮助！?

教师简介

?? ? ? ?? ?

黄剑芳，笔名氢剑，在福建省福州第一中学任教高中化学，中学高级教师，教学基本功扎实，有较强的学科整合能力，上课、说课、课件比赛均获过全国一等奖，多篇论文在《化学教育》、《化学教学》等刊物上发表，近年专注三维技术应用于物质结构的教学研究。兴趣广泛，喜爱登山、徒步、摄影、旅游，知识面广，授课风趣幽默，待人真诚，深受广大师生欢迎。

微课视频及讲解文字说明

本文微视频时长29分钟07秒。利用三维虚拟技术动态演绎金属晶体4中基本堆积方式形成过程，全面、系统而又有创意地分析4种晶胞占有的原子个数、配位数及空间利用率等问题。化抽象为形象，讲解简明扼要，想象力丰富，富有启发性。

以下文字供观看视频参考，但视频有更多的细节。

金属原子只有少数的价电子能用于成键，这样少的价电子不足于使金属晶体中原子间形成经典的共价键或离子键，因此金属在形成晶体时倾向于组成极为紧密的结构，使金属的原子轨道具有最大程度的重叠而稳定。在金属晶体中，金属原子如同半径相等的小球一样，一个挨一个地紧密堆积成晶体。

一、金属晶体的原子堆积模型

1、一维紧密堆积方式只有1种，如图1所示。

图1一维紧密堆积

2、二维堆积有3种常见方式，可看作将一维紧密堆积复制“一条”后将其逆时针分别旋转90°、60°、70.53°得到由“两条”?一维紧密堆积按上述夹角形成的二维堆积“框架”，沿水平方向将“框架”铺成面，分别得到行列对齐“四球一空”的非密置层a、行列相错“三球一空”的密置层b以及介于二者之间“四球一空”的半密置层c（图2）。?

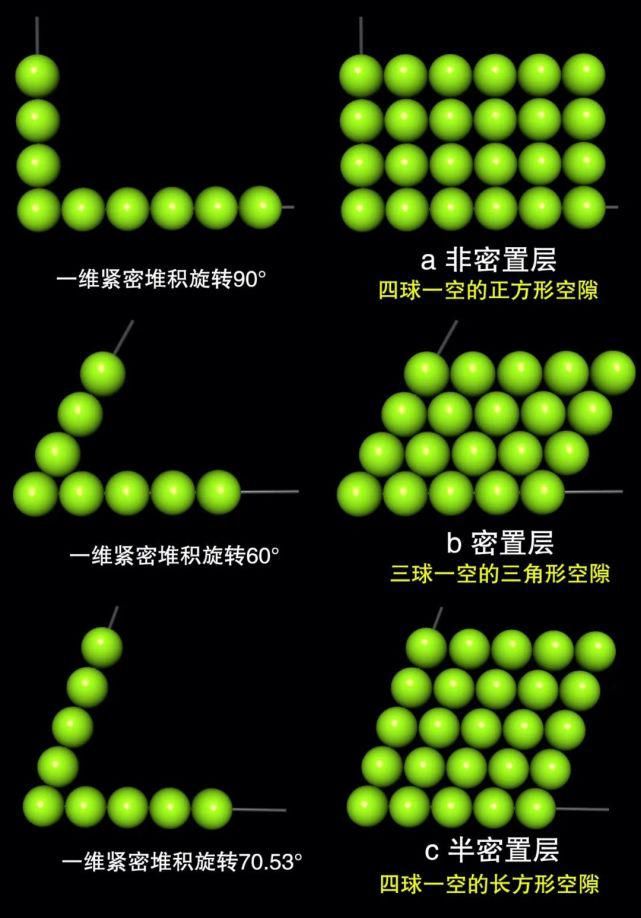图2按90°、60°、70.53°夹角构建的3种常见二维堆积方式

3、三维堆积得到金属晶体的4种基本堆积模型

（1）简单立方堆积

简单立方堆积基于非密置层形成，即相邻非密置层原子核行列对齐堆积，两层完成一个周期，这样的堆积方式叫简单立方堆积，形成简单立方晶胞（图3）。简单立方堆积空隙大，空间利用率较低，不属于紧密堆积方式。

图3简单立方晶胞

（2）体心立方堆积

体心立方亦不属于最紧密堆积，但空间利用率又高于简单立方，根源在于金属原子在二维空间放置时既未采用简单立方行列对齐“四球一空”的非密置层堆积方式，也未采用六方或面心立方行列错位“三球一空”的密置层堆积方式，而是介于二者之间行列夹角为70.53°的“半密置层”堆积方式，形成的空隙为“四球一空”的长方形状（见图2）。

以现有的“半密置层”为第一层，在第一层上方将金属原子放置在“四球一空”的长方形状空隙中心形成第二层，第三层的球投影与第一层的球重合，两层完成一个周期，这样的堆积方式叫体心立方堆积，形成体心立方晶胞（图4）。

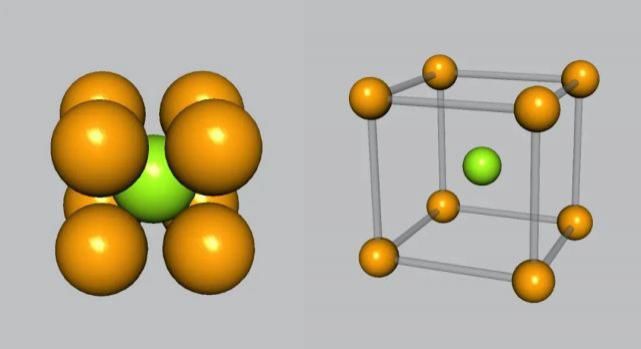图4体心立方晶胞

（3）六方最密堆积

六方最密堆积基于密置层形成，密置层“三球一空”的空隙形状像三角形，六方最密堆积就是基于密置层按一定规律在三维空间堆积而成的。

我们以任意一个金属球体为基准展开来说明，每个金属原子与周围6个金属原子形成6个三角形状的空隙（图5），细看这些三角形有两种朝向，一种是1、3、5这样倒立的三角形状空隙，另一种是2、4、6这样正立的三角形状空隙，以现有的密置层为第一层，在第一层上方将金属原子放置在2、4、6正立的三角形状空隙内形成第二层，若第三密置层的球投影与第一密置层的球重合，两层完成一个周期，这样的最密堆积方式叫六方最密堆积，形成六方晶胞（图6）。

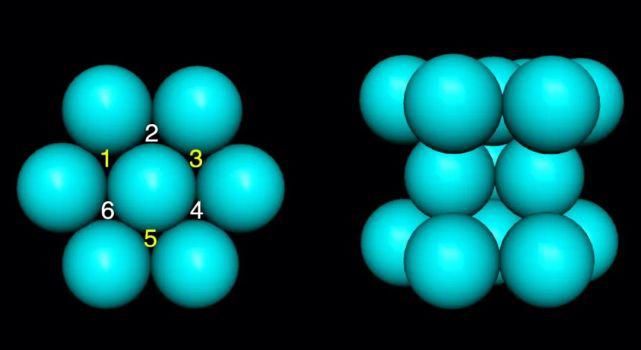图5“三球一空”的密置层

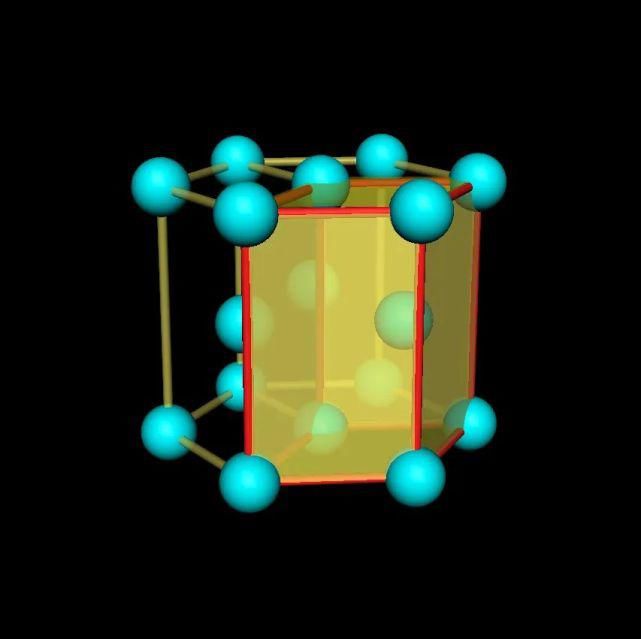图6六方最密堆积（红色棱边围成的是晶胞）

（4）立方最密堆积

立方最密堆积亦基于密置层形成。由于每个金属原子与周围6个金属原子形成6个三角形状的空隙，这些三角形有两种朝向，一种是1、3、5这样倒立的三角形状空隙，另一种是2、4、6这样正立的三角形状空隙（如图7），以现有的密置层为第二层，在第二层上方将金属原子放置在1、3、5倒立的三角形状空隙内形成第一层，在第二层下方将金属原子放置在2、4、6正立的三角形状空隙内形成第三层。三层完成一个周期，这样的最密堆积方式叫立方最密堆积，形成面心立方晶胞（如图8）。

文章来源：《化学教与学》 网址: http://www.hxjyxzz.cn/zonghexinwen/2020/0811/472.html